Reproduced with
the permission
of Metrologia.

An important note
about this version

ITS-90 Text

Contents

1. Units of Temperature and Introduction from Metrologia 27, 3-10 (1990)
2. Principles of the International Temperature Scale of 1990 (ITS-90)
3. Definition of the International Temperature Scale of 1990
4. Supplementary Information and Differences from Earlier Scales & Appendix

• List of Tables

3. Definition of the International Temperature Scale of 1990

Between 0.65 K and 5.0 K T₉₀ is defined in terms of the vapour-pressure temperature relations of ³He and ⁴He.

Between 3.0 K and the triple point of neon (24.5561 K) T₉₀ is defined by means of a helium gas thermometer calibrated at three experimentally realizable temperatures having assigned numerical values (defining fixed points) and using specified interpolation procedures.

Between the triple point of equilibrium hydrogen (13.8033 K) and the freezing point of silver (961.78°C) T₉₀ is defined by means of platinum resistance thermometers calibrated at specified sets of defining fixed points and using specified interpolation procedures.

Above the freezing point of silver (961.78°C) T₉₀ is defined in terms of a defining fixed point and the Planck radiation law.

The defining fixed points of the ITS-90 are listed in Table 1. The effects of pressure, arising from significant depths of immersion of the sensor or from other causes, on the temperature of most of these points are given in Table 2.

3.1. From 0.65 K to 5.0 K: Helium Vapour-Pressure Temperature Equations

In this range T₉₀ is defined in terms of the vapour pressure p of ³He and ⁴He using equations of the form:

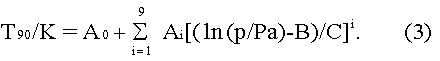
The values of the constants A0, Ai, B and C are given in Table 3 for ³He in the range of 0.65 K to 3.2 K, and for ⁴He in the ranges 1.25 K to 2.1768 K (the point) and 2.1768 K to 5.0 K.

3.2. From 3.0 K to the Triple Point of Neon (24.5561 K): Gas Thermometer

In this range T₉₀ is defined in terms of a ³He and ⁴He gas thermometer of the constant-volume type that has been calibrated at three temperatures. These are the triple point of neon (24.5561 K), the triple point of equilibrium hydrogen (13.8033 K), and a temperature between 3.0 K and 5.0 K. This last temperature is determined using a ³He or a ⁴He vapour pressure thermometer as specified in Sect. 3.1.

3.2.1. From 4.2 K to the Triple Point of Neon (24.5561 K) with ⁴He as the Thermometric Gas. In this range T₉₀ is defined by the relation:

T₉₀ = a + bp +cp²,        (4)

where p is the pressure in the gas thermometer and a, b and c are coefficients the numerical values of which are obtained from measurements made at the three defining fixed points given in Sect. 3.2, but with the further restriction that the lowest one of these points lies between 4.2 K and 5.0 K.

3.2.2. From 3.0 K to the Triple Point of Neon (24.5561 K) with ³He or ⁴He as the Thermometric Gas. For a ³He gas thermometer, and for a ⁴He gas thermometer used below 4.2 K, the non-ideality of the gas must be accounted for explicitly, using the appropriate second virial coefficient B₃ (T₉₀)or B4 (T₉₀ ). In this range T₉₀ is defined by the relation:

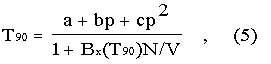
where p is the pressure in the gas thermometer a, b and c are coefficients the numerical values of which are obtained from measurements at three defining temperatures as given in Sect. 3.2, N/V is the gas density with N being the quantity of gas and V the volume of the bulb, x is 3 or 4 according to the isotope used, and the values of the second virial coefficients are given by the relations:

For ³He

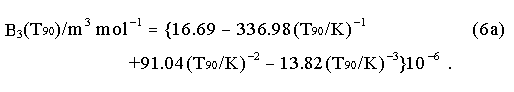
For ⁴He

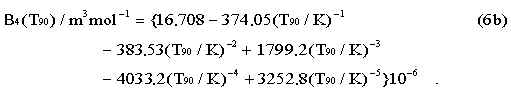
The accuracy with which T₉₀ can be realized using Eqs. (4) and (5) depends on the design of the gas thermometer and the gas density used. Design criteria and current good practice required to achieve a selected accuracy are given in "Supplementary Information for the ITS-90".

3.3. The Triple Point of Equilibrium Hydrogen
(13.8033 K) to the Freezing Point of Silver (961.78°C):
Platinum Resistance Thermometer

In this range T₉₀ is defined by means of a platinum resistance thermometer calibrated at specified sets of defining fixed points, and using specified reference and deviation functions for interpolation at intervening temperatures.

No single platinum resistance thermometer can provide high accuracy, or is even likely to be usable, over all of the temperature range 13.8033 K to 961.78°C. The choice of temperature range, or ranges, from among those listed below for which a particular thermometer can be used is normally limited by its construction.

For practical details and current good practice in particular concerning types of thermometer available, their acceptable operating ranges, probably accuracies, permissible leakage resistance, resistance values, and thermal treatment, see "Supplementary Information for the ITS-90". It is particularly important to take account of the appropriate heat treatments that should be followed each time a platinum resistance thermometer is subjected to a temperature above about 420°C.

Temperatures are determined in terms of the ratio of the resistance R (T₉₀)at a temperature T₉₀ and the resistance R (273.16 K) at the triple point of water. This ratio,

W(T₉₀),is: ²

W(T₉₀) = R (T₉₀)/R(273.16 K).       (7)

An acceptable platinum resistance thermometer must be made from pure, strain-free platinum, and it must satisfy at least one of the following two relations:

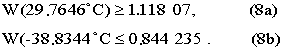
An acceptable platinum resistance thermometer that is to be used up to the freezing point of silver must also satisfy the relation:

In each of the resistance thermometer ranges, T₉₀ is obtained from Wr (T₉₀) as given by the appropriate reference function {Eqs. (9) or (10)}, and the deviation W (T₉₀) - Wr (T₉₀). At the defining fixed points this deviation is obtained directly from the calibration of the thermometer: at intermediate temperatures it is obtained by means of the appropriate deviation function {Eqs. (12), (13) and (14)}.

(i) - For the range 13.8033 K to 273.16 K the following reference function is defined:

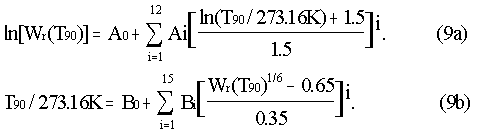
An inverse function, equivalent to Eq. (9a) to within 0.1 mK, is Eq 9b

The values of the constants A0, Ai, B0, and Bi, are given in Table 4.

A thermometer may be calibrated for use throughout this range or, using progressively fewer calibration points, for ranges with low temperature limits of 24.5561 K, 54.3584 K and 83.8058 K, all having an upper limit of 273.16 K.

(ii) - For the range 0°C to 961.78°C the following reference function is defined:

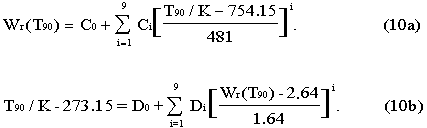
The values of the constants Co, Ci, Do and Di are given in Table 4.

A thermometer may be calibrated for use throughout this range or, using fewer calibration points, for ranges with upper limits of 660.323°C, 419.527°C, 231.928°C, 156.5985°C or 29.7646°C, all having a lower limit of 0°C.

(iii) - A thermometer may be calibrated for use in the range 234.3156 K (-38.8344°C) to 29.7646°C, the calibration being made at these temperatures and at the triple point of water. Both reference functions {Eqs. (9) and (10)} are required to cover this range.

The defining fixed points and deviation functions for the various ranges are given below, and in summary form in Table 5.

3.3.1. The Triple Point of Equilibrium Hydrogen (13.8033 K) to the Triple Point of Water (273.16 K). The thermometer is calibrated at the triple points of equilibrium hydrogen (13.8033 K), neon (24.5561 K), oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K), and water (273,16 K), and at two additional temperatures close to 17.0 K and 20.3 K. These last two may be determined either: by using a gas thermometer as described in sect. 3.2, in which case the two temperatures must lie within the ranges 16.9 K to 17.1 K and 20.2 K to 20.4 K respectively; or by using the vapour pressure-temperature relation of equilibrium hydrogen, in which case the two temperatures must lie within the ranges 17.025 K to 17.045 K and 20.26 K to 20.28 K respectively, with the precise values being determined from Eqs. (11a) and (11b) respectively:

T₉₀/K - 17.035 = (p/kPa - 33.3213)/13.32       (11a)

T₉₀/K - 20.27 = (p/kPa - 101.292)/30 .              (11b)

The deviation function is ³:

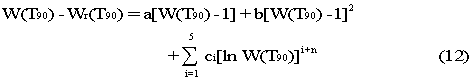
with values for the coefficients a, b and ci being obtained from measurements at the defining fixed points and with n=2.

For this range and for the sub-ranges 3.3.1.1 to 3.3.1.3 .the required values of Wr (T₉₀) are obtained from Eq. (9) or from Table 1.

3.3.1.1 The Triple Point of Neon (24.5561 K) to the Triple Point of Water (273.16K). The thermometer is calibrated at the triple points of equilibrium hydrogen (13.8033 K), neon (24.5561 K), oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K) and water (273,16 K).

The deviation function is given by Eq. (12) with values for the coefficients a, b, c1, c2 and c3 being obtained from measurements at the defining fixed points and with c4 = c5 = n = 0.

3.3.1.2.The Triple Point of Oxygen (54.3584 K) to the Triple Point of Water (273.16 K). The thermometer is calibrated at the triple points of oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K) and water (273.16 K).

The deviation function is given by Eq. (12) with values for the coefficients a, b and c1, being obtained from measurements at the defining fixed points, with c2= c3= c4,= c5,=0 and with n=1.

3.3.1.3. The Triple Point Of Argon (83.8058 K) to the Triple Point of Water (273.16K). The thermometer is calibrated at the triple points of argon (83.8058 K), mercury (234.3156 K) and water (273.16 K).

The deviation function is:

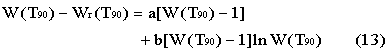
with the values of a and b being obtained from measurements at the defining fixed points.

3.3.2. From 0°C to the Freezing Point of Silver (961.78°C). The thermometer is calibrated at the triple point of water (0.01°C), and at the freezing points of tin (231.928°C), zinc (419.527°C), aluminium 660.323°C) and silver (961.78°C).

The deviation function is:

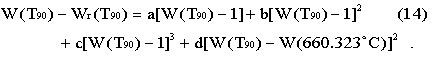
For temperatures below the freezing point of aluminium d=0, with the values of a, b and c being determined from the measured deviations from Wr (T₉₀)at the freezing points of tin, zinc and aluminium. From the freezing point of aluminium to the freezing point of silver the above values of a, b and c are retained and the value of d is determined from the measured deviation from Wr (T₉₀) at the freezing point of silver.

For this range and for the sub-ranges 3.3.2.1 to 3.3.2.5 the required values for Wr(T₉₀) are obtained from Eq. (10) or from Table 1.

3.3.2.1. From 0°C to the Freezing Point of Aluminium (660.323°C). The thermometer is calibrated at the triple point of water (0.01°C), and at the freezing points of tin (231.928°C), zinc (419.527°C) and aluminium (660.323 °C).

The deviation function is given by Eq. (14), with the values of a, b and c being determined from measurements at the defining fixed points and with d=0.

3.3.2.2. From 0°C to the Freezing Point of Zinc (419.527°C). The thermometer is calibrated at the triple point of water (0.01°C), and at the freezing points of tin (231.928°C) and zinc (419.527°C).

The deviation function is given by Eq. (14) with the values of a and b being obtained from measurements at the defining fixed points and with c=d=0.

3.3.2.3. From 0°C to the Freezing Point of Tin (231.928°C). The thermometer is calibrated at the triple point of water (0.01°C), and at the freezing points of indium (156.5985°C) and tin (231.928°C).

The deviation function is given by Eq. (14) with the values of a and b being obtained from measurements at the defining fixed points and with c = d = 0.

3.3.2.4. From 0°C to the Freezing Point of Indium (156.5985°C). The thermometer is calibrated at the triple point of water (0.01 °C), and at the freezing point of indium (156.5985°C).

The deviation function is given by Eq. (14) with the value of a being obtained from measurements at the defining fixed points and with b = c = d = 0.

3.3.2.5. From 0°C to the Melting Point of Gallium (29.7646°C). The thermometer is calibrated at the triple point of water (0.01 °C), and at the melting point of gallium (29.7646°C).

The deviation function is given by Eq. (14) with the value of a being obtained from measurements at the defining fixed points and with b = c = d = 0.

3.3.3. The Triple Point of Mercury (-38.8344°C) to the Melting Point of Gallium (29.7646°C). The thermometer is calibrated at the triple points of mercury (-38.8344°C), and water (0.01°C), and at the melting point of gallium (29.7646°C).

The deviation function is given by Eq. (14) with the values of a and b being obtained from measurements at the defining fixed points and with c=d=0.

The required values of Wr (T₉₀) are obtained from Eqs. (9 b) and (10b) for measurements below and above 273.16 K respectively, or from Table 1.

3.4. The Range Above the Freezing Point of Silver

(961.78°C): Planck Radiation Law

Above the freezing point of silver the temperature T₉₀ is defined by the equation:

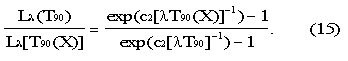
where T₉₀(X) refers to any one of the silver { T₉₀ (Ag) =1234.93K}, the gold { T₉₀ (Au)=1337.33K} or the copper { T₉₀ (Cu) = 1357.77 K} freezing points ⁴ and in which
L T₉₀ and L [T₉₀ (X)] are the spectral concentrations of the radiance of a blackbody at the wavelength (in vacuo) at T₉₀, and at T₉₀, (X) respectively, and c2 = 0.014388 metre Kelvin.

For practical details and current good practice for optical pyrometry, see "Supplementary Information for the ITS-90" (BIPM-1990).

² Note that this definition of W (T₉₀) differs from the corresponding definition used in the ITS-27, ITS-48, IPTS-48, and IPTS-68: for all of these earlier scales W(T) was defined in terms of a reference temperature of 0°C, which since 1954 has itself been defined as 273.15 K

³ This deviation function {and also those of Eqs. (13) and (14)} may be expressed in terms of Wr, rather than W; for this procedure see "Supplementary information for ITS-90"

⁴The T₉₀ values of the freezing points of silver, gold and copper are believed to be self consistent to such a degree that the substitution of any one of them in place of one of the other two as the reference temperature T₉₀(X) will not result in significant differences in the measured values of T₉₀.

© 1999 and Legal